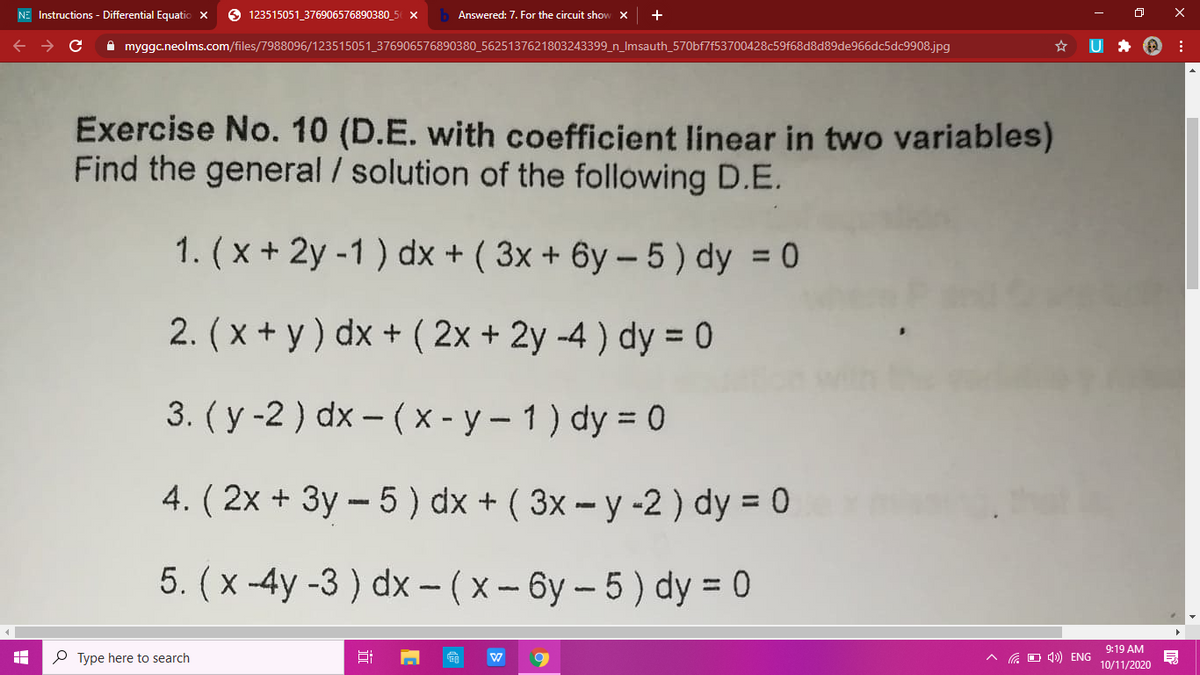
Transcribed image text Solve the equation (3x?
(x-y-2)dx+(x-2y-3)dy=0-Solution for y(x^2xy2y^2)dxx(3y^2xyx^2)dy=0 solve using homogeneous equations Q The volume of a right circular cone of radius a and height y is given by V ' = ma²ySuppose that A From the given problem;One obtains a new equation which is P (x,y)dx Q (x,y)dy =0, with P = 1 y^2/x^2 1/x^2 Q = 1 2y/x This equation is an exact differential dF (x,y) = 0 because P_y = 2y/x^2 = Q_x The solution is F (x,y) = C with F_x = P = 1 y^2/x^2 1/x^2 F_y = Q = 1 2y/x
(x-y-2)dx+(x-2y-3)dy=0のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  |  |
 |  | |
「(x-y-2)dx+(x-2y-3)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「(x-y-2)dx+(x-2y-3)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 | 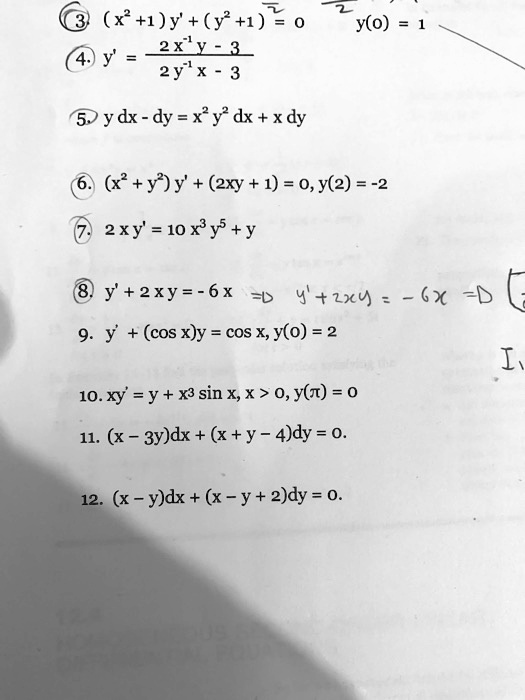 | |
「(x-y-2)dx+(x-2y-3)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 | 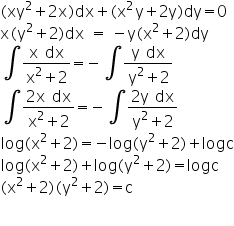 | |
「(x-y-2)dx+(x-2y-3)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
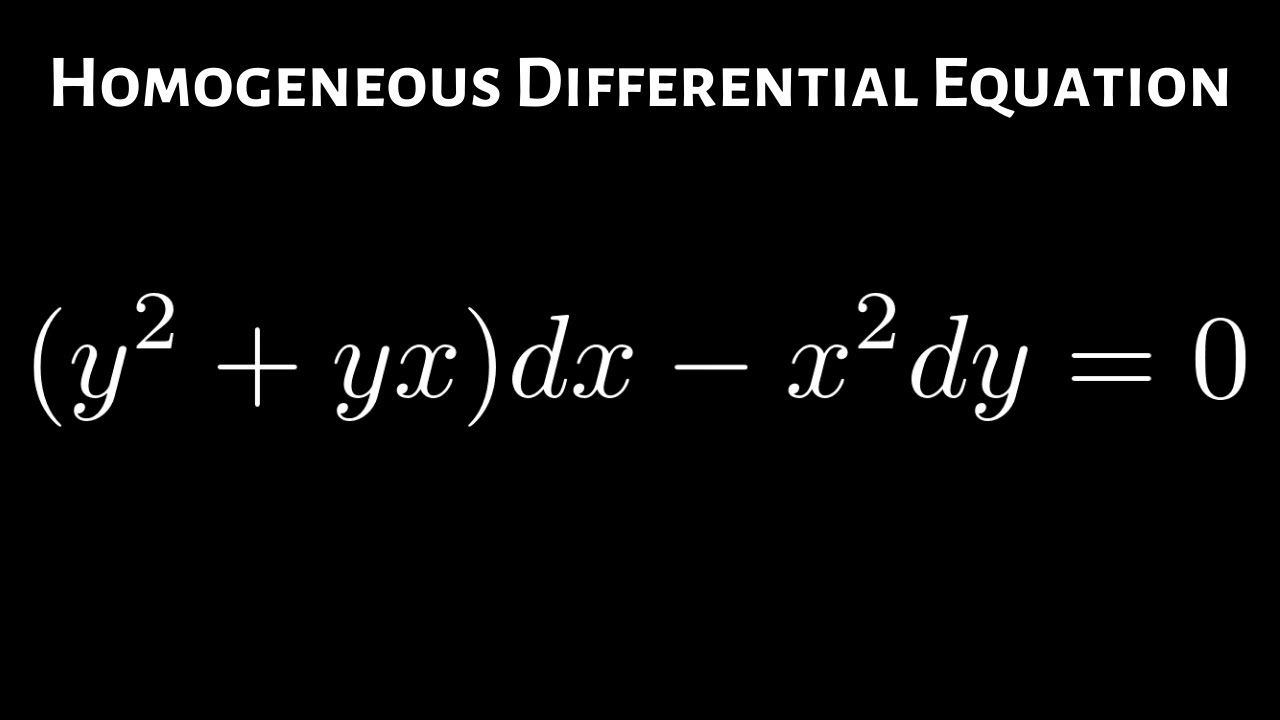 | ||
 |  |  |
 |  | |
「(x-y-2)dx+(x-2y-3)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  |  |
「(x-y-2)dx+(x-2y-3)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 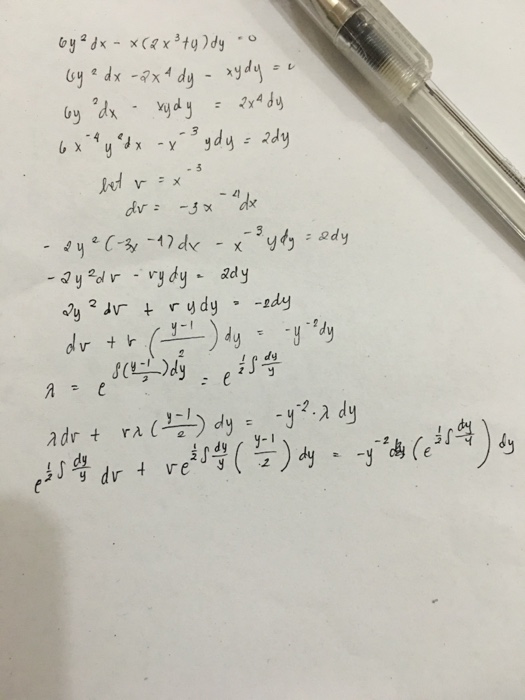 | |
 |  | |
 |  | |
「(x-y-2)dx+(x-2y-3)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
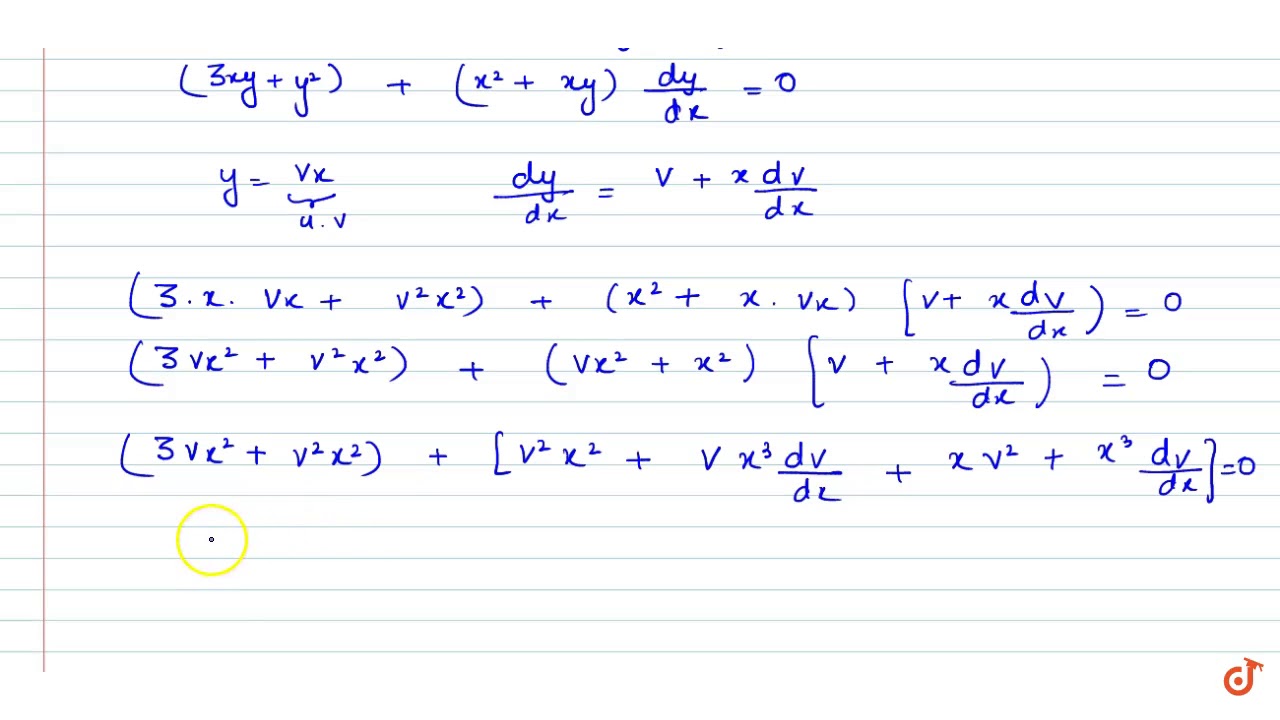 | ||
「(x-y-2)dx+(x-2y-3)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |
See the answer See the answer See the answer done loading By Integrating Factors y (2x – y 1)dx x (3x – 4y 3)dy = 0 (x 2 y 2 1)dx x (x – 2y)dy = 0 (4xy 3y 2 – x)dx x (x 2y)dy = 0 y (x y 1)dx x (x 3y 2)dy = 0 y 2 dx (3xy y 2 –See the answer See the answer See the answer done loading
Incoming Term: (x-y-2)dx+(x-2y-3)dy=0, 4. (x-y-2)dx+(x-2y-3)dy=0, 11. (x-y-2)dx+(x-2y-3)dy=0, (x^3+xy^2)dx+(x^2y+y^3)dy=0, (x-y-2)dx-(2x-2y-3)dy=0, solve (x^3+xy^2)dx+(x^2y+y^3)dy=0, 3x(xy-2)dx+(x^3+2y)dy=0, (y^2-3y-x)dx+(2y-3)dy=0, x^2 y dx-(x^3+y^3)dy=0, (x ^ 2 * y - 2x * y ^ 2) * dx - (x ^ 3 - 3x ^ 2 * y) * dy = 0,




0 件のコメント:
コメントを投稿